MOE scaling laws

https://arxiv.org/pdf/2502.05172 loss scaling law: \begin{equation*} L(N_{act}, D, \hat{E}) = 35.91\hat{E}^{0.2285}N_{act}^{0.1889-0.0098\ln(\hat{E})} + 35.98\hat{E}^{-0.5529}D^{0.1775+0.0259\ln(\hat{E})} + 1.3637 \end{equation*}

learning rate scaling formula: $LR(N_{act\text{e}},E)=exp(8.39-0.81\ln (N_{act\text{e}})-0.25\ln (E))$ where:

• L represents the final training loss.
• LR represents the learning rate
• $N_{act}$ denotes the number of active parameters
• D is the dataset size, in terms of training token number
• E is the number of experts

i like this statement tbh

compute optimiality

most of the compute optimality depends on the number of experts and not really the dataset size and model size i mean they are proportional but to get the minimum loss on a compute constraint i think we can trade off on them these were there training budgets and tests that they did here $N_{act}^{opt}$ is the optimal number of active params and $D^{opt}$ is the optimal number of tokens in the dataset 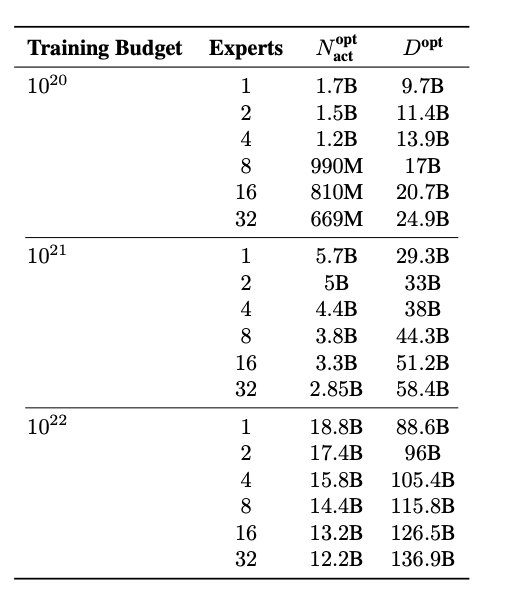we can infer as we increase the number of experts the active param gets smaller (obviously) but we also have to increase the dataset size accordingly for good loss. there must be some ratios for the active param too let’s read (this is chinchilla functional btw so calculations should be easier)

nanoMOE ftw

nano MOE deets

according to the scaling laws we can calculate the amount of compute token needed to efficiently train a model of same param size but better loss but since we are trying to implment depseek v3 style there are a few difference (shared experts finegrained experts) which im not sure how we can take that into context although by the given trend the more the number of experts the better the training loss im thinking this would apply the same for shared and finegrained experts with some overhead in training cost and number of tokens to train on. the current rule with the given compute constraint and number of params has been: although they did this conservatively the actual scaling happens at less than E times the dataset also they try to keep number of experts < 8 since after that the loss becomes unpredictable due to the token:param ratio

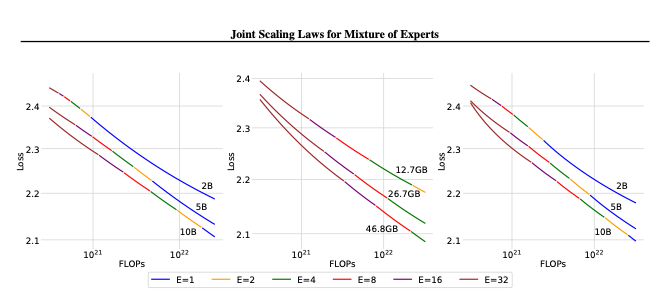
so mainly v3 has four differences

• shared experts
• multi latent attention
• multi token prediction might create an overhead in number of tokens but if we are taking the E times the dataset we should be on course with same compute similarly for shared experts although im not sure how much memory overhead this would cause us. lets talk model specifics now for nano moe we have decided that the model param would be 135M params trying to compete with smol lm so we need to find the compute/tokens required/optimal_experts